Obtaining QY values for DAE

and equivalent power for a given QY

Import the experiment Data

import pandas as pd

exp_data = pd.read_csv("DATA/DAE.csv")

exp_data

	timestamp	cycle	type	186.85486	187.31995223015844	187.78500323297956	188.250012996982	188.71498151068454	189.17990876260572	189.64479474126426	...	1032.9632529736894	1033.3204920667242	1033.6776665334785	1034.034776362471	1034.3918215422202	1034.7488020612445	1035.1057179080635	1035.4625690711953	1035.8193555391586	1036.176077300472
0	2025-04-04 11:29:32.797890	1	zero	16.990556	24978.543889	249.154361	241.872694	253.523361	243.935833	258.499167	...	652.315972	654.500472	655.471361	647.218806	664.694806	659.354917	666.151139	657.049056	657.049056	657.049056
1	2025-04-04 11:31:06.034842	1	on	16.990556	24978.543889	254.858333	231.395185	276.163951	261.600617	252.431111	...	639.168519	672.070864	642.944198	664.789198	651.034938	650.495556	633.235309	639.707901	639.707901	639.707901
2	2025-04-04 11:31:07.075687	1	on	16.990556	24978.543889	240.025309	238.676852	256.206790	239.755617	265.106605	...	653.192469	652.922778	643.483580	663.710432	668.834568	634.853457	628.111173	670.452716	670.452716	670.452716
3	2025-04-04 11:31:08.109308	1	on	16.990556	24978.543889	242.991914	246.767593	242.182840	280.479012	280.748704	...	637.820062	659.665062	663.440741	645.641111	635.662531	629.189938	638.359444	631.347469	631.347469	631.347469
4	2025-04-04 11:31:09.153691	1	on	16.990556	24978.543889	241.643457	222.765062	271.039815	262.140000	255.667407	...	652.113704	651.844012	651.574321	651.034938	648.877407	647.528951	638.629136	645.101728	645.101728	645.101728
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
614	2025-04-04 11:41:43.804611	1	on	16.990556	24978.543889	241.913148	236.789012	220.337840	231.934568	246.767593	...	649.686481	641.326049	641.865432	641.865432	641.056358	645.371420	639.438210	631.347469	631.347469	631.347469
615	2025-04-04 11:41:44.858569	1	on	16.990556	24978.543889	212.786481	231.125494	234.361790	239.755617	265.106605	...	638.089753	626.762716	630.268704	636.201914	634.853457	648.068333	654.001543	662.361975	662.361975	662.361975
616	2025-04-04 11:41:45.888795	1	on	16.990556	24978.543889	223.304444	240.564691	237.058704	251.622037	240.295000	...	659.125679	635.392840	641.056358	646.719877	642.135123	654.540926	630.268704	648.338025	648.338025	648.338025
617	2025-04-04 11:41:46.925455	1	on	16.990556	24978.543889	232.204259	234.631481	235.170864	257.824938	243.800988	...	621.368889	644.292654	632.156543	629.459630	631.617160	652.653086	630.808086	632.426235	632.426235	632.426235
618	2025-04-04 11:41:59.961864	1	static	16.990556	24978.543889	225.488944	217.964556	231.557000	247.455306	278.281028	...	634.475889	630.228250	649.888750	648.675139	633.990444	646.247917	634.111806	643.213889	643.213889	643.213889

619 rows × 2051 columns

Get important data from dataframe

import numpy as np

intensities=np.array(exp_data[(exp_data["type"] != "zero") & (exp_data["type"] != "static")].iloc[:, 3:], dtype=np.float64)
static=np.array(exp_data[(exp_data["type"]== "static")].iloc[:, 3:], dtype=np.float64)[0]
zero=np.array(exp_data[(exp_data["type"]== "zero")].iloc[:, 3:], dtype=np.float64)[0]
wavelengths = np.array(exp_data.columns[3:], dtype=np.float64)
timestamps = pd.to_datetime(exp_data["timestamp"][(exp_data["type"] != "zero") & (exp_data["type"] != "static")]) # Convert timestamp strings to datetime objects
timestamps = np.array((timestamps - timestamps.iloc[0]).dt.total_seconds()) # Convert to seconds since the first timestamp

def compute_absorbance(intensities: np.ndarray, static: np.ndarray, zero: np.ndarray) -> np.ndarray:
    EPS = 1e-12
    num = intensities - static
    den = np.maximum(zero - static, EPS)  # Éviter division par zéro
    absorbance = -np.log10(np.maximum(num / den, EPS))  # Éviter log(0) ou log(négatif)
    return absorbance

absorbance = compute_absorbance(intensities, static, zero)

Plotting

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import matplotlib.cm as cm
# Set global style
plt.style.use("ggplot")  # Clean style

fig, axs = plt.subplots(1, 3, figsize=(18, 5))
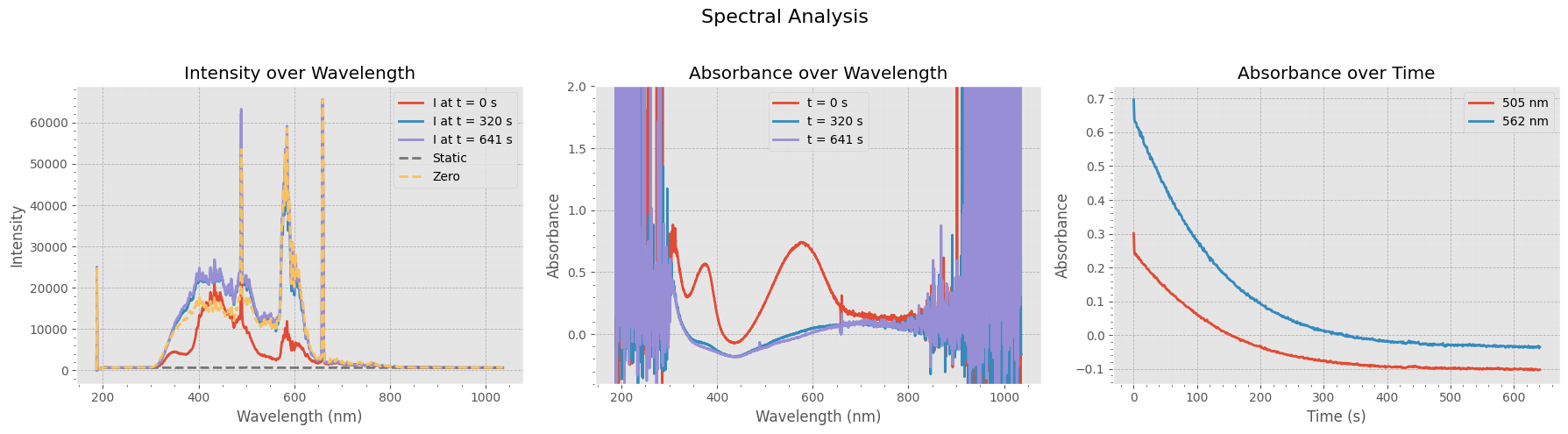
fig.suptitle("Spectral Analysis", fontsize=16)

# --- Intensity Plot ---
axs[0].plot(wavelengths, intensities[0, :], label=f"I at t = {timestamps[0]:.0f} s", linewidth=2)
axs[0].plot(wavelengths, intensities[len(intensities)//2, :], label=f"I at t = {timestamps[len(intensities)//2]:.0f} s", linewidth=2)
axs[0].plot(wavelengths, intensities[-1, :], label=f"I at t = {timestamps[-1]:.0f} s", linewidth=2)
axs[0].plot(wavelengths, static, '--', label="Static", linewidth=2)
axs[0].plot(wavelengths, zero, '--', label="Zero", linewidth=2)
axs[0].set_title("Intensity over Wavelength")
axs[0].set_xlabel("Wavelength (nm)")
axs[0].set_ylabel("Intensity")
axs[0].legend()
axs[0].grid(True, which='major', linestyle='--', linewidth=0.6, color='gray', alpha=0.5, zorder=0)
axs[0].minorticks_on()
axs[0].grid(True, which='minor', linestyle=':', linewidth=0.3, color='lightgray', alpha=0.4, zorder=0)
# --- Absorbance Plot ---
axs[1].plot(wavelengths, absorbance[0, :], label=f"t = {timestamps[0]:.0f} s", linewidth=2)
axs[1].plot(wavelengths, absorbance[len(absorbance)//2, :], label=f"t = {timestamps[len(absorbance)//2]:.0f} s", linewidth=2)
axs[1].plot(wavelengths, absorbance[-1, :], label=f"t = {timestamps[-1]:.0f} s", linewidth=2)
axs[1].set_title("Absorbance over Wavelength")
axs[1].set_xlabel("Wavelength (nm)")
axs[1].set_ylabel("Absorbance")
axs[1].set_ylim(-0.4, 2)
axs[1].legend()
axs[1].grid(True, which='major', linestyle='--', linewidth=0.6, color='gray', alpha=0.5, zorder=0)
axs[1].minorticks_on()
axs[1].grid(True, which='minor', linestyle=':', linewidth=0.3, color='lightgray', alpha=0.4, zorder=0)
# --- Absorbance vs Time Plot ---
WL = [505, 562]
idxs = [np.argmin(np.abs(wavelengths - wl)) for wl in WL]

for i, idx in enumerate(idxs):
    axs[2].plot(timestamps, absorbance[:, idx], label=f"{wavelengths[idx]:.0f} nm", linewidth=2)

axs[2].set_title("Absorbance over Time")
axs[2].set_xlabel("Time (s)")
axs[2].set_ylabel("Absorbance")
axs[2].legend()
axs[2].grid(True, which='major', linestyle='--', linewidth=0.6, color='gray', alpha=0.5, zorder=0)
axs[2].minorticks_on()
axs[2].grid(True, which='minor', linestyle=':', linewidth=0.3, color='lightgray', alpha=0.4, zorder=0)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()

Clean Data :

# Define wavelength range of interest
wavelength_range = [560, 565]
idx_range = np.argmin(np.abs(wavelengths[:, None] - wavelength_range), axis=0)

# Extract and normalize absorbance data within the wavelength range
absorbance_subset = absorbance[:, idx_range[0]:idx_range[1]]
absorbance_subset -= np.min(absorbance_subset)
wavelengths_subset = wavelengths[idx_range[0]:idx_range[1]]

# Filter out specific time points (e.g., first frame and last 300 entries)
# Adjust indices as needed
time_filter_indices = [0] + list(range(-300, 0))
absorbance_subset = np.delete(absorbance_subset, time_filter_indices, axis=0)
timestamps_filtered = np.delete(timestamps, time_filter_indices)

# Create subplots
fig, axs = plt.subplots(1, 3, figsize=(18, 5))

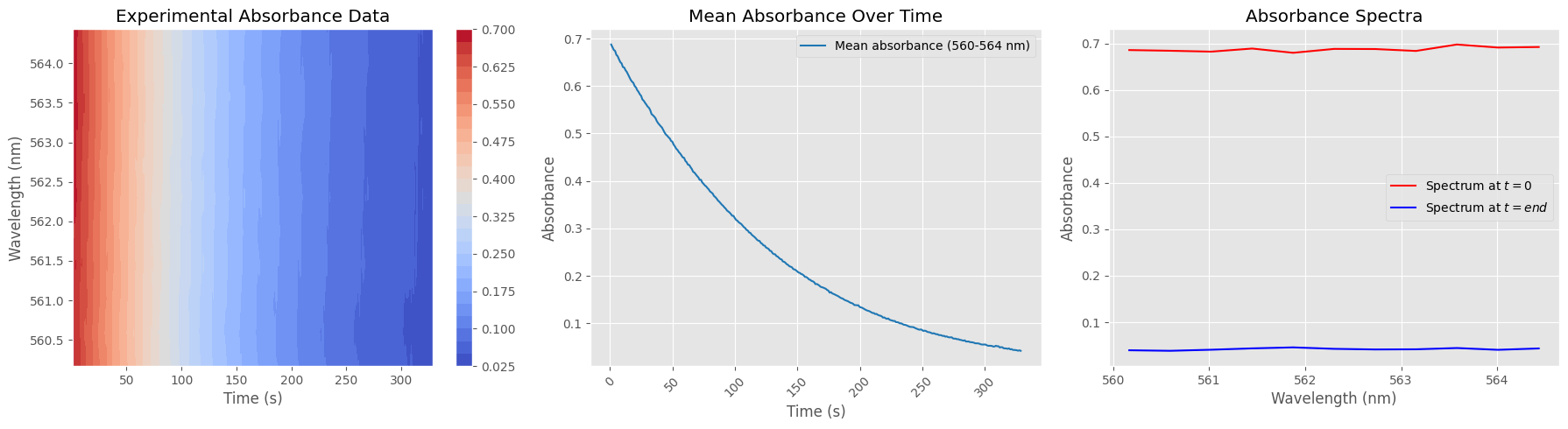
# --- 1. Absorbance Heatmap ---
X, Y = np.meshgrid(timestamps_filtered, wavelengths_subset)
contour = axs[0].contourf(X, Y, absorbance_subset.T, levels=30, cmap="coolwarm")
axs[0].set_title("Experimental Absorbance Data")
axs[0].set_xlabel("Time (s)")
axs[0].set_ylabel("Wavelength (nm)")
fig.colorbar(contour, ax=axs[0])

# --- 2. Absorbance Over Time (Averaged Across Wavelength Range) ---
mean_absorbance = np.mean(absorbance_subset, axis=1)
axs[1].plot(timestamps_filtered, mean_absorbance, label=f"Mean absorbance ({wavelengths_subset[0]:.0f}-{wavelengths_subset[-1]:.0f} nm)", color='tab:blue')
axs[1].set_title("Mean Absorbance Over Time")
axs[1].set_xlabel("Time (s)")
axs[1].set_ylabel("Absorbance")
axs[1].tick_params(axis="x", rotation=45)
axs[1].legend()
axs[1].grid(True)

# --- 3. Absorbance Spectrum at Start and End ---
axs[2].plot(wavelengths_subset, absorbance_subset[0, :], label="Spectrum at $t=0$", color='red')
axs[2].plot(wavelengths_subset, absorbance_subset[-1, :], label="Spectrum at $t=end$", color='blue')
axs[2].set_title("Absorbance Spectra")
axs[2].set_xlabel("Wavelength (nm)")
axs[2].set_ylabel("Absorbance")
axs[2].legend()
axs[2].grid(True)

plt.tight_layout()
plt.show()

Fit to get QY

from scipy.integrate import solve_ivp
from scipy.optimize import curve_fit

# Physics constants :

h = 6.62607004 * 10 ** (-34)
NA = 6.02214086 * 10 ** (23)
c_vaccum = 299792458
wl = 505 # nm
v = c_vaccum / (wl * 1e-9)
volume = 14e-4 # L
l = 1 # cm
eps_closed_505 = 0.6e4 # M-1 . cm-1
eps_closed_562 = 1.1e4 # M-1 . cm-1
I_w_list = [14.21e-3*0.92, 14.27e-3]
for I_w in I_w_list:
    C_exp = mean_absorbance/(eps_closed_562*l)
    
    C0 = C_exp[0]
    
    I_0 = I_w  / (h * v * NA) / volume # mole de photons.L-1
    print(I_0)
    
    def f(t, C_closed, QY_CF2OF):
        # Con[Con<0]=0
        Iabs_CF =  I_0 * (1 - np.exp(- eps_closed_505 * C_closed * l * np.log(10)))
        dCCF_deri = -QY_CF2OF * Iabs_CF 
        # print(f"Con = {Con}, dC = {dCon_deri}, t = {t}")
        return dCCF_deri
    
    def fi(t, q1, c):
        sol = solve_ivp(f, t_span, y0, args=(q1,), t_eval=timestamps_filtered)
        if not sol.success:
            print("⚠️ solve_ivp failed:", sol.message)
            return None  # Retourne None en cas d'échec
        return sol.y.flatten()#+c
    
    
    
    QY = 0.0233
    initial_guess = (QY, 1)
    bounds = ([0, -1],  [1, 1])
    
    t_span = [timestamps_filtered[0], timestamps_filtered[-1]]
    y0 = np.array([C0])
    # y = solve_ivp(f, t_span, y0, args=(QY,), t_eval=timestamps)
    
    print("Reg start")
    popt, pcov = curve_fit(fi, timestamps_filtered, C_exp, p0=initial_guess, bounds=bounds)
    uncertainties = np.sqrt(np.diag(pcov))
    
    # Print results
    print("=== Fit Results ===")
    for i, (coef, incert) in enumerate(zip(popt, uncertainties), start=1):
        print(f"Parameter {i}: {coef:.4f} ± {incert:.4f}")
    
    # Compute fitted values
    fitted_values = fi(timestamps_filtered, *popt)
    litt_values = fi(timestamps_filtered, QY,0)
        
    
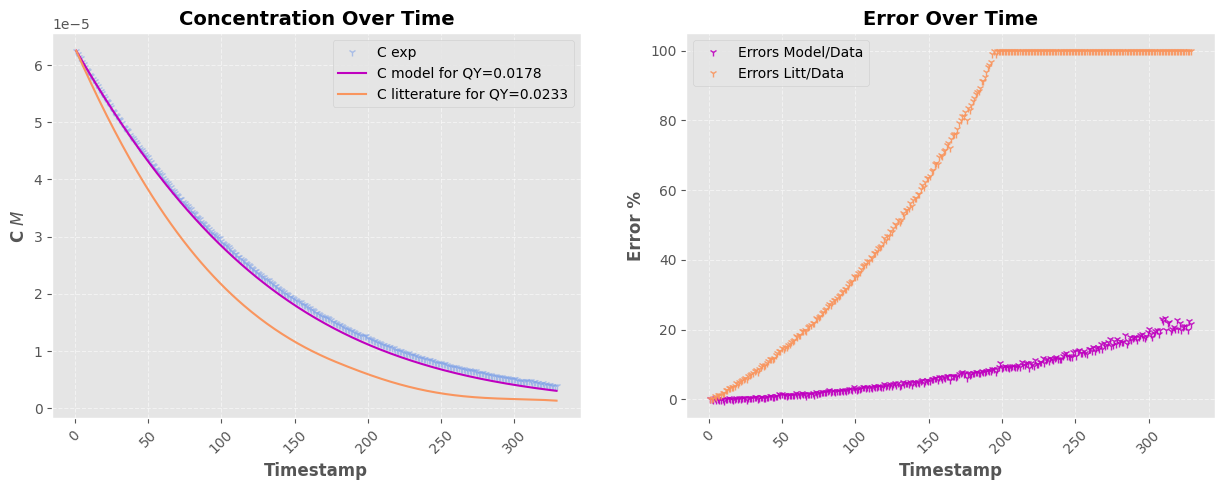
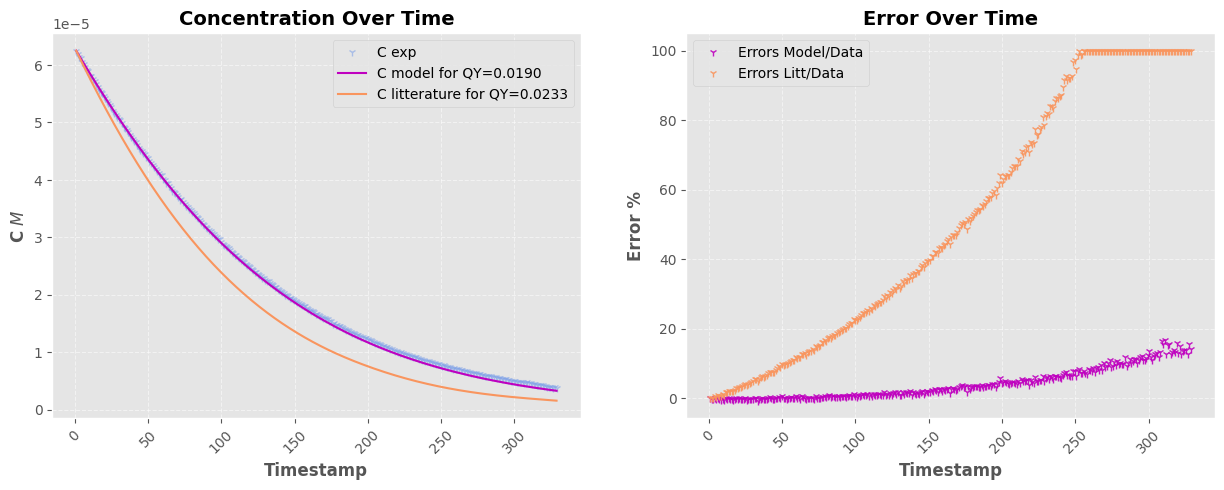
    fig, a = plt.subplots(1, 2, figsize=(15, 5))
    pastel_colors = ["m", "#f9955e", "#81a3e8"]  # Mauve, orange, sky blue

    # First Plot - Concentration Over Time
    a[0].plot(timestamps_filtered, C_exp, "1", color=pastel_colors[2], label="C exp", alpha=0.6)
    a[0].plot(timestamps_filtered, fitted_values, "-", color=pastel_colors[0], label=f"C model for QY={popt[0]:0.4f}")
    a[0].plot(timestamps_filtered, litt_values, "-", color=pastel_colors[1], label=f"C litterature for QY={QY}")

    
    a[0].set_xlabel("Timestamp", fontsize=12, fontweight="bold")
    a[0].set_ylabel("C $M$", fontsize=12, fontweight="bold")
    a[0].set_title("Concentration Over Time", fontsize=14, fontweight="bold")
    a[0].tick_params(axis="x", rotation=45)
    a[0].grid(linestyle="--", alpha=0.5)
    a[0].legend()
    
    # Second Plot - Error Over Time
    a[1].plot(timestamps_filtered, (C_exp - fitted_values) * 100 / C_exp, "1", color=pastel_colors[0], label="Errors Model/Data", alpha=0.9)
    ERR = (C_exp - litt_values) * 100 / litt_values
    ERR[ERR > 100] = 100
    ERR[ERR < -100] = -100
    a[1].plot(timestamps_filtered, ERR, "1", color=pastel_colors[1], label="Errors Litt/Data", alpha=0.9)
    
    a[1].set_xlabel("Timestamp", fontsize=12, fontweight="bold")
    a[1].set_ylabel("Error %", fontsize=12, fontweight="bold")
    a[1].set_title("Error Over Time", fontsize=14, fontweight="bold")
    a[1].tick_params(axis="x", rotation=45)
    a[1].grid(linestyle="--", alpha=0.5)
    a[1].legend()
    
    plt.show()

3.9420090134680676e-05
Reg start
=== Fit Results ===
Parameter 1: 0.0190 ± 0.0000
Parameter 2: 1.0000 ± 0.0000

4.302884421732194e-05
Reg start
=== Fit Results ===
Parameter 1: 0.0178 ± 0.0000
Parameter 2: 1.0000 ± 0.0000